UNIDAD II: DISTRIBUCIONES MUESTRALES
El estudio de determinadas características de una población se efectúa a través de diversas muestras que pueden extraerse de ella.
El muestreo puede hacerse con o sin reposición, y la población de partida puede ser infinita o finita. Una población finita en la que se efectúa muestreo con reposición puede considerarse infinita teóricamente. También, a efectos prácticos, una población muy grande puede considerarse como infinita. En todo nuestro estudio vamos a limitarnos a una población de partida infinita o a muestreo con reposición.
μ =(Miu) Media de una población
N =Número total de elementos de la población
σ2 = Varianza
σ = Desviación estándar o Desviación típica
x= Media de una muestra
n = Número total de elementos de la muestra
Teorema del límite central.
Una máquina llena bolsas de cubrebocas con un contenido medio de
150 gr y una varianza de 120 grs 2 Si se toma una muestra de 40 bolsas, ¿Cuál
es la probabilidad de que la media muestral esté entre 145 y 152 grs?
P(145 ≤ X ≤ 152)
P=(145-150/(10.9544/√40 ) ) = -2.89 = 0.00193
P=(152-150/(10.9544/√40 ) ) = 1.15 = 0.87493
= 0.87493-0.00193 = 0.873
= 0.873 * 100%= 87.3%
El peso de un producto en Kg sigue una distribución normal con media 30 y
desviación típica 3 kg Un empresario decide aceptar un lote de 600 unidades
que le envía el proveedor, si al elegir 5 unidades de dicho producto al azar
encuentra que su peso medio no es menor que 29 kg Calcular la probabilidad
de que se rechace el lote?
P( X ≤ 29)
P=(29-30/(3/√5 ) ) = -0.7453 = 0.22965
= 0.22965 = 22.97%
= 22.3%
Un banco llevó una estadística de los reclamos de los clientes en todas sus
sucursales y vio que está distribuido normalmente, con una media de 305
reclamos por año y una desviación estándar de 27 reclamos Obtenga la
probabilidad de que una muestra aleatoria de 33 sucursales se tengan 290
reclamos por año
P( X ≤ 290)
P=(290-305/(27/√33 ) ) = -3.191 = 0.00071
= 0.00071 * 100%= 0.071%
11. Una empresa de mensajería que opera en la ciudad tarda una media de 35
minutos en llevar un paquete, con una desviación típica de 8 minutos
Supongamos que durante el día de hoy han repartido 20 paquetes
a)
¿Cuál es la probabilidad de que la media de los tiempos de entrega de hoy
esté mayor a 40 minutos?
P( X ≤ 40)
P=(10-35/(8/√20 ) ) = 2.7950 = 0.99736
= 1- 0.99736 = 0.00264
= 0.00264 * 100%= 0.26%
Ciertos tubos fabricados por una compañía, tienen una duración media de
900 horas y una desviación estándar de 70 horas Si se seleccionan
aleatoriamente una muestra de 36 tubos, ¿cual es la probabilidad de que dichos
tubos tengan una duración media entre 𝑥1= 870 y 𝑥2= 925 horas?


P(870 ≤ X ≤ 925)
P=(870-900/(70/√36 ) ) = 2.5714 = 0.00508
P=(925-900/(70/√36 ) ) = 2.142 = 0.98382
= 0.98382 - 0.00508= 0.9787
= 0.9787 * 100%= 97.87%
La edad de los miembros de una determinada asociación sigue una
distribución normal N Sabemos que la distribución de las medias de las edades
en muestra de tamaño 36 tienen como media 52 años y como desviación típica
15 años
¿Cuál
es la probabilidad de que un miembro de la asociación, elegido al azar
sea mayor de 60 años?
P(X ≥ 60)
P=(60-52/(15/√36 ) ) = 3.2 = 0.99931
= 1 - 0.99931= 0.00069
= 0.00069 * 100%= 0.069%
En la clase de estadística la media de un examen bimestral es de 80 puntos
con una desviación estándar de 12 puntos Si la distribución de notas es normal
y en la clase hay 35 alumnos
¿Cuál es la probabilidad de que haya obtenido una nota entre 75 y 85 puntos?
P(75 ≤ X ≤ 85)
P1=(75-80/(12/√35 ) ) = -2.4650 = 0.0695
P2=(85-80/(12/√35 ) ) = 2.4650 = 0.99305
= 0.99305 - 0.0695= 0.9861
= 0.9861 * 100%= 98.61%
Una máquina llena bolsas de chocolates con un contenido medio de 160 gr y
una varianza de 110 grs 2 Si se toma una muestra de 35 bolsas, ¿Cuál es la
probabilidad de que la media muestral esté entre 140 y 172 grs
P(140 ≤ X ≤ 172)
P1=(140-160/(10.48/√35 ) ) = -0.3225 = 0.37448
P2=(172-160/(10.48/√35 ) ) = 0.1935 = 0.57535
= 0.57535 - 0.37448= 0.2008
=0.2008 * 100%= 20.08%
Ciertos artículos fabricados por una compañía, tienen una duración media
de 800 horas y una desviación estándar de 65 horas Si se seleccionan
aleatoriamente una muestra de 40 tubos, ¿Cuál es la probabilidad de que dichos
tubos tengan una duración media entre 670 y 925 horas?
P(670 ≥ X ≤ 925)
P1=(670-800/(65/√40 ) ) = -0.3162 = 0.37828
P2=(925-800/(65/√40 ) ) = 0.30 = 0.61791
= 0.61791 - 0.37828= 0.2396
=0.2396 * 100%= 23.96%
Una empresa eléctrica fabrica focos que tienen una duración que se
distribuye aproximadamente en forma normal, con media de 800 horas y
desviación estándar de 40 horas Encuentre la probabilidad de que una muestra
aleatoria de 16 focos tenga una vida promedio de menos de 775 horas?
P(X ≤ 795)
P1=(795-800/(40/√16 ) ) = -0.1562 = 0.44038
= 1 - 0.44038= 0.5596
=0.5596 * 100%= 55.96%



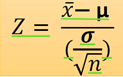



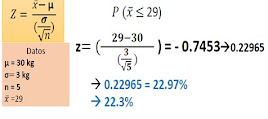










No hay comentarios.:
Publicar un comentario